Полученная тем или иным способом запись условной кривой не характеризует явления в целом, а только некоторую его сторону. Она может отражать изменение давления - это будет кривая давления, объёма участка тела - объёмная кривая. С её помощью можно зарегистрировать скорость, с которой происходят изменения давления или объёма - это будет скоростная или дифференциальная кривая, разлагающая явление по составляющей времени. Наконец, нас может заинтересовать изменение скорости в единицу времени или же ускорение, которое испытывает масса ткани при движении. Это может быть представлено кривой ускорения.

Рассматривая подобные кривые, связанные с движением крови по артериальным сосудам, следует постоянно помнить об основной и важнейшей стороне явления: ток крови имеет пульсирующий характер. При каждой систоле сердца возникает некоторый прирост объёма и давления в артериальной системе и ускорение движения крови в артериях. К концу диастолы система приходит в исходное состояние, которое нарушается новой систолой – поступлением новой массы крови в аорту.

Если посмотреть на кривые давления, сфигмограммы и реограммы, то между ними трудно найти специфические внешние различия. Для правильного понимания такого неслучайного сходства следует рассмотреть механизмы возникновения данных кривых.

В результате сокращения в систолу сердце с определённым ускорением выбрасывает некую массу крови в магистральные сосуды, создавая дополнительный запас энергии в виде пульсового давления. Пульсирующая кровь передаёт свои колебания на мембрану датчика, запись которых осуществляют с помощью регистрирующего устройства. Кривую давления чаще всего получают, располагая датчик в просвете сосуда. При этом следует учитывать, что энергия давления в растяжимом сосуде распространяется многовекторно, поэтому кривая давления регистрирует не общее давление, а то, которое направлено перпендикулярно мембране датчика (давление напора по ходу сосуда).

Сфигмограмма оценивает те же события, используя стенку сосуда. Правда, следует помнить, что регистрируется одна из составляющих общего давления – боковое давление. При продвижении пульсовой волны или волны давления артериальная стенка растягивается, деформируется. Степень деформации на каждом ограниченном отрезке сосуда в определённый момент времени будет определяться свойствами и состоянием сосудистой стенки и величиной давления крови. По существу, пульсовая кривая характеризует деформацию сосудистой стенки в данном ограниченном участке, возникающую под влиянием давления крови.

Реограмма – это та же кривая бокового давления, полученная иным путём. Всякая энергия стремится к самосохранению, поэтому она устремляется туда, где её затрата будет наименьшей. При систолическом выбросе кровь частично движется по ходу сосуда, создавая давление напора. В силу того, что её скорость превышает линейную скорость кровотока, она, наталкиваясь на инерцию медленно движущейся крови, перераспределяется на более податливую растяжимую стенку артерии, увеличивая её просвет. Пульсирующее изменение просвета сосуда создаёт эффект электрического проводника с переменным сечением, что и регистрируется реографом. Таким образом, кривую бокового давления получают через меняющуюся проводимость пульсирующей крови.

Следует отметить ещё одно большое сходство между первой производной реограммы и допплерограммой того же сосуда. Допплерографическая кривая оценивает линейную скорость кровотока по ходу сосуда, используя ультразвуковой луч, отражённый от движущейся крови. Дифференциальная реограмма оценивает скорость изменения просвета сосуда за счёт пульсового притока крови. Иными словами оценивается линейная скорость кровотока по направлению к стенке сосуда.

Вторая производная реограммы или кривая ускорения практически не используется в медицинских программах. А ведь она может дать полезную дополнительную информацию о событиях в магистральных сосудах и лучше их понять.

С этой целью мною после сканирования оцифровано несколько реограмм с помощью программы GetData Graph Digitizer. В работе использованы реограммы, оценённые по традиционной методике, как нормальные или с некоторыми патологическими синдромами.

Все последующие расчёты и построения кривых осуществлены с помощью опций, заложенных в программе Excel.

Цель: сравнительный анализ кривых объёмной реограммы и её первой и второй производных

Амплитудные значения объёмной реограммы (РГ) измерялись в Омах.

Первая производная реограммы или реограмма скорости (РГ скорости, Ом/сек) вычислялась по формуле:

v = d/t

Здесь: d – прирост (снижение) амплитуды объёмной реограммы за интервал времени t.

Вторая производная или реограмма ускорения (РГ ускорения, Ом/сек^-2) вычислялась по формуле:

a = v/t

Вторая производная оценивает прирост скорости за интервал времени.

Учитывая то, что абсолютные цифровые значения скорости и ускорения существенно выше, чем у объёмной кривой, для размещения их на одной диаграмме проведено масштабирование первой и второй производной относительно объёмной реограммы. Масштаб подобран эмпирически и составляет для кривой скорости 1:20 и для кривой ускорения 1:750.

На данном этапе основной задачей является выяснение механизмов формирования пульсовой волны. С моей точки зрения, местом образования первичной пульсовой волны следует считать аорту в самом её начале, поэтому все события, участвующие в её формировании, происходят в непосредственной близости. Отсюда первичная волна распространяется по всем магистральным артериям, в которых приобретает незначительные локальные изменения.

Реографическую кривую оценивают по амплитудным, временны́м составляющим и их производным: скорости и ускорению.

Как правило, вся кривая разбивается на определённые временны́е отрезки с учётом событий, происходящих в сердце и сосудах. Гемодинамические колебания в сосудах зависят непосредственно от работы сердца и меняются по периодам и фазам. Реографическая кривая может быть использована для фазового анализа сердца, однако основным её предназначением является оценка свойств стенки сосуда (растяжимости, эластичности, тонуса), его кровенаполнения, а также оттока крови по периферическим сосудам (периферического сосудистого сопротивления).

На реограмме выделяют периоды систолы и диастолы, которые в свою очередь разбиваются на более короткие временны́е интервалы (фазы) по наличию подъёмов и впадин на объёмной кривой и её производных.

Рисунок VI-1а, в, с. Нормальная РЭГ-кривая.

 

Традиционно всякая реограмма делится на две неравные части – анакроту и катакроту. Начальная часть бегущей по артерии пульсовой волны (анакрота) начинается крутым подъёмом. Катакротическая часть волны имеет более продолжительный пологий спуск.

Для справки: наивысшие точки подъёмов называют максимальными экстрéмами (extréme max), самые глубокие точки впадин называют минимальными экстрéмами (extréme min). Когда речь идёт о максимумах и минимумах, то отсчёт ведётся не от изолинии, а от предыдущей впадины или подъёма. Максимальный экстрéм может находиться ниже изолинии, а минимальный – выше. Их поиск на пульсовой кривой без первой и второй производных часто затруднителен.

Каждому экстрéму на пульсовой кривой и её производных соответствует то или иное событие в сердечно-сосудистой системе. Амплитудные измерения осуществляются в определённых точках, поэтому некоторые из них имеют буквенные названия. В медицинской диагностической литературе для этого чаще всего используют заглавные буквы русского алфавита. Некоторым точкам, не имевшим ранее буквенных обозначений, названия даны мною.

На сосудистую стенку постоянно действуют силы извне и изнутри. Трансмуральное давление характеризует разность между внутренним и внешним давлением на любой мембране (стенке).

Какая бы большая сила не действовала на сосудистую стенку изнутри, если ей противодействует равная по величине сила снаружи, то стенка сосуда будет оставаться нерастянутой. При самом минимальном давлении, если между внутренними и внешними силами возникнет неравенство (градиент), сосуд растянется или сократится. Следовательно, величина растяжения сосудистой стенки прямо пропорциональна градиенту давления.

Если внутреннее давление формируется, прежде всего, в результате систолического выброса, то противодействие слагается из общих внешних сил (атмосферное давление), давления окружающих тканей. Ещё одна сила, противодействующая растяжению, заложена в стенке сосуда. Это её растяжимость, базальный тонус.

В систолу градиент давления возрастает в пользу внутренних сил, сосуд растягивается. На максимуме растяжения наступает точка гемодинамического равновесия, в которой силы действия равны силам противодействия, градиент давления равен 0. После того как внешние силы превысят внутриартериальное давление, сосуд начнёт сокращаться (отрицательный градиент давления). В конце диастолы внутриартериальное давление значительно больше того, которое действует снаружи, поэтому сосуд не спадается полностью. Превышение составляет примерно 1,1*10⁴ Н*м^-2 (80 мм.рт.ст.).

В анакроту внутренняя сила преобладает над внешней (положительный градиент давления). Её величина зависит от:

Рассмотрим подробнее каждую составляющую.

От этого соотношения сил действия и противодействия и зависит, какое количество силы будет направлено в сторону стенки, а какое по ходу. Эти два вектора играют роль “сообщающихся сосудов”. Чем больше сопротивления по ходу сосуда, тем большая часть силы сердечного выброса участвует в растяжении стенки сосуда, и наоборот.

На конечностях давление внешних тканей на сосуды может проявиться при выраженном отёке, лимфостазе.

В данном перечне не рассматривается воздействие на сосуды атмосферного давления, поскольку его влияние учтено во всех исходных показателях. Давление в сосудах и сердце, как в систолу, так и диастолу, измеряется относительно атмосферного.

 

 

На объёмной кривой мы можем оценить относительную величину и направления действующей силы.

 

 

В анакроту реографическая кривая поднимается из точки Д₀ к точке А, сосудистая стенка постоянно растягивается, силы действия преобладают над силами противодействия. Однако по пульсовой кривой невозможно оценить динамику процесса. Для этого необходимо использовать кривые скорости и ускорения.

На приведенной реограмме (рис VI-2) умышленно удлинены временны́е интервалы, поэтому прирост (спад) объёмной кривой происходит ступенчато. Это сделано для лучшей наглядности динамики растяжения (сужения) сосуда. Высота каждой ступени соответствует приросту амплитуды объёмной кривой за равный интервал времени. Хотя все временны́е отрезки одинаковы, ступени имеют разную высоту.

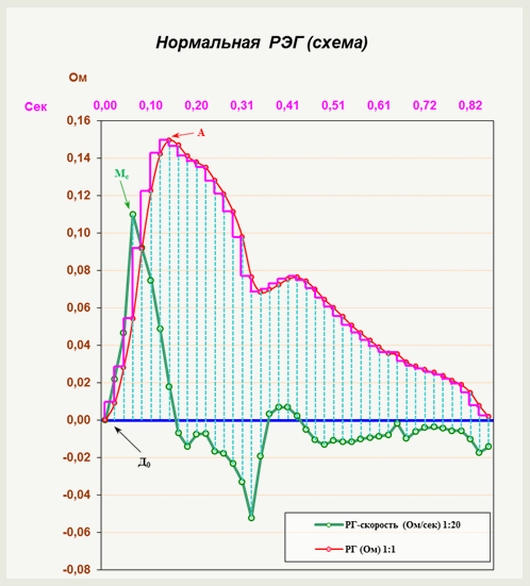
Рисунок VI-2. Амплитуда – скорость

 

Первая производная оценивает скорость растяжения сосудистой стенки за тот или иной временной отрезок. В нашем примере скорость растяжения равна отношению высоты ступени к её длине. Если бы ступени были одинаковой высоты на всём протяжении анакроты, то скорость второй и всех последующих ступеней были бы равны скорости первой. Анакрота на объёмной кривой отражалась бы прямой линией под некоторым углом к нулевой. Первая производная регистрировалась бы прямой линией, параллельной изолинии, находящейся на высоте первой ступени. Это указывало бы на то, что на всем протяжение анакроты действует одинаковый градиент давления.

Однако, скорость растяжения сосуда неравномерная. Рассмотрим на примере динамику скорости в сопоставлении с приростом амплитуды объёмной кривой. Поскольку временны́е отрезки ступеней одинаковые, то, чем больше высота ступени, тем выше скорость. На анакроте она возрастает от ступени к ступени. Максимальная скорость соответствует ступени, имеющей наибольшую высоту (точка М_с). Затем прирост амплитуды начинает уменьшаться, что ведёт к снижению скорости. При приближении к вершине анакроты (точка А) высота ступеней существенно снижается, скорость приближается к 0. В максимальной точке объёмной реографической кривой прирост амплитуды отсутствует, поэтому кривая скорости достигает нулевой отметки.

Если сопоставить скорость с градиентом давления, то максимальная скорость растяжения (точка М_с) возникает при максимальном градиенте давления. Наивысшая точка (extréme max) анакроты (А) соответствует пику максимального растяжения сосудистой стенки. В этот момент наступает гемодинамическое равновесие, когда градиент давления равен 0, силы действия равны силам противодействия.

На нисходящей части реограммы (катакроте) первая производная рассчитывается по тем же принципам, однако со знаком минус (ступени здесь идут вниз). Это значит, что внешние силы берут верх над внутренними, растянутая сосудистая стенка сокращается. Кривая скорости находится ниже изолинии, наиболее глубокой точке скорости соответствует ступень на пульсовой кривой с наибольшей величиной спада. По мере уменьшения спада ступеней кривая скорости будет приближаться к изолинии снизу. В самой низшей точке инцизуры на катакроте (extréme min) спад амплитуды объёмной кривой прекратится, поэтому кривая скорости достигнет нулевой отметки. Вновь наступит гемодинамическое равновесие, градиент давления будет равен 0. Затем первая производная может вновь стать положительной, если на объёмной кривой начнётся подъём.

 

 

Вторая производная оценивает прирост скорости за единицу времени или же ускорение.

Проиллюстрируем сказанное. Два автомобиля движутся с одинаковой скоростью 90км/час. Первый достиг этой скорости за 10сек, второй – за 6сек. Следовательно, у второго автомобиля прирост скорости за секунду был выше.

Два сосуда имеют одинаковую максимальную скорость растяжения. Однако первый достиг её через 55мс, второй – через 45мс. Следовательно, второй имел бóльший прирост скорости за единицу времени. Как было сказано выше, максимальной скорости растяжения соответствует максимальный градиент давления. Во втором случае последний был достигнут быстрее. Согласно законам механики прирост скорости пропорционален приросту силы. Следовательно, во втором случае прирост силы за единицу времени был бóльшим, чем в первом.

На приведенной реограмме (рис VI-3) временны́е интервалы умышленно удлинены, поэтому ступенчатый подъём (спад) первой производной, позволяет более наглядно оценить динамику прироста скорости. Хотя все временны́е отрезки одинаковы, ступени имеют разную высоту. Высота каждой ступени соответствует приросту скорости растяжения (сужения) сосуда за равный интервал времени или же ускорению.

В нашем примере ускорение равно отношению высоты ступени к её длине. Если бы высота ступеней была одинаковой на всём протяжении анакроты, то ускорение второй и всех последующих ступеней были бы равны ускорению первой. Первая производная отражалась бы прямой линией под некоторым углом к нулевой. Вторая производная регистрировалась бы прямой линией, находящейся на высоте первой ступени, параллельно изолинии. Это указывало бы на то, что на всём протяжение данного временнóго отрезка прирост силы одинаковый.

Однако скорость растяжения сосуда неравномерна. Для оценки динамики прироста (спада) скорости сопоставим первую и вторую производные на приведенном примере. Поскольку временны́е отрезки ступеней одинаковые, то, чем больше высота ступени, тем больше прирост скорости. В начале систолы скорость прирастает. Максимальное ускорение соответствует ступени, имеющей наибольшую высоту. Затем прирост скорости начинает уменьшаться, что ведёт к спаду кривой ускорения. При приближении к максимальному экстрéму первой производной высота ступеней существенно снижается, ускорение приближается к 0. В точке М_с прирост скорости отсутствует, поэтому кривая ускорения достигает нулевой отметки.

Рисунок VI-3. Скорость – ускорение

 

Максимальному ускорению соответствует максимальный прирост силы. Для стенки сосуда эквивалентом силы является градиент между внутренним и внешним давлением. Прирост градиента давления возможен либо в результате усиления сил действия, либо в результате ослабления сил противодействия, и наоборот.

При растяжении сосуда возрастают как внутренние силы действия, так и внешние силы противодействия. На восходящей линии первого положительного зубца ускорения (У₁₊) противодействие сосудистой стенки минимальное, однако сила сердечного выброса не достигла своего максимума (рис. VI-1c). На нисходящей линии этого зубца внутренние силы достигла достаточно высоких значений, однако при этом возросло и сопротивление сосудистой стенки. Поэтому extréme max данного зубца на кривой ускорения соответствует времени наиболее оптимального для внутренних сил соотношения сил действия и противодействия, при котором происходит наибольший прирост внутреннего градиента давления.

На нисходящей части кривой скорости вторая производная рассчитывается по тем же принципам, однако ступени здесь идут вниз (со знаком -). Это значит, что происходит замедление скорости. Кривая ускорения находится ниже изолинии, а наибольшее отрицательное ускорение соответствует ступени на первой производной с наибольшим спадом. По мере уменьшения спада ступеней кривая ускорения будет приближаться к изолинии снизу. В самой низшей точке первой производной (extréme min) спад амплитуды кривой скорости прекратится, поэтому кривая ускорения достигнет нулевой отметки снизу.

На нисходящей линии отрицательного зубца ускорения У₁- силы противодействия сосудистой стенки набрали достаточный потенциал, однако внутренние силы хотя и снизились, но ещё достаточно высоки. На восходящей линии этого зубца внутренние силы снизились до минимума, однако темп прироста потенциальных сил сосудистой стенки упал. Поэтому extréme min данного зубца на кривой ускорения соответствует времени наименее оптимального для внутренних сил соотношения сил действия и противодействия, при котором происходит наибольший спад внутреннего градиента давления.

Следует помнить, что пока первая производная регистрируется выше изолинии, то на второй производной оценивают темп прироста и спада положительного градиента давления. Если кривая скорости регистрируется ниже изолинии, то на кривой ускорения видна динамика прироста и спада отрицательного градиента давления. Её интерпретируют по тем же принципам, в зеркальном отображении. Отрицательный градиент прирастает, если кривая ускорения опускается, и, наоборот, спадает, если вторая производная поднимается. Иными словами, чем дальше вторая производная находится вниз от изолинии, тем больший прирост отрицательного градиента давления.

 

 

В систолу сердце выбрасывает определённую массу крови с некоторым ускорением, создавая прирост давления в сосудистом русле. Основной вектор силы изначально направлен прямолинейно по ходу сосуда и передаёт часть своей энергии в виде продольной пульсовой волны, преодолевая инерцию. Другая часть перераспределяется в сторону растяжимой стенки сосуда, создавая поперечную (пульсовую волну). Эти два вектора играют роль “сообщающихся сосудов”. Чем больше сопротивления по ходу, тем большая часть силы сердечного выброса перераспределяется в сторону стенки сосуда, и наоборот.

Свой подъём анакрота начинает из точки Д₀, находящейся на изолинии, и заканчивается в точке А, в которой сосудистая стенка достигает наибольшего растяжения. Величина амплитуды в этой точке зависит от распределения внутренних сил в сторону стенки (величины сопротивления по ходу сосуда) и от свойств сосудистой стенки (растяжимости, тонуса).

Итак, амплитуда пульсовой кривой в точке А возрастёт, если

 

Вся анакрота делится на два временны́х отрезка.

Первый отрезок Д₀ – М соответствует фазе быстрого изгнания. Пульсовая кривая прирастает наиболее динамично, внутренние силы существенно превышают внешние. Сердце выбрасывает кровь с наибольшей силой, а нерастянутые сосуды оказывают наименьшее противодействие. На второй производной данный период анакроты отражается зубцом У₁₊ (рисунок VI-1с), верхняя точка которого соответствует наибольшему приросту положительного градиента давления. С этого момента прирост скорости, а потому и силы, происходит меньшим темпом. С приближением к точке М скорость растяжения стенки сосуда достигает максимума. Поскольку в extréme max первой производной прирост скорости прекращается, то кривая ускорения достигает нулевой отметки. В точке М_с регистрируется максимальный положительный градиент давления.

Увеличение амплитуд первой производной в точке М_с и второй производной в точке У₁₊ происходит по тем же причинам, что и у пульсовой кривой, если

Второй отрезок анакроты М – А соответствует началу фазы медленного изгнания. Сосудистая стенка продолжает растягиваться, но скорость растяжения прогрессивно снижается. Сила сердечного выброса падает, а сила противодействия упругой стенки сосуда возрастает. В точке А кривая первой производной достигает нулевой отметки. На второй производной данному периоду анакроты соответствует зубец У_1- (рисунок VI-1с). Его extréme min соответствует временнóму отрезку наибольшего падения скорости, а потому и наибольшего падения градиента давления.

Итак, если зубец У_1- на кривой ускорения углубился, то это указывает на возросший спад положительного градиента давления, которому могли способствовать

 

«Водоразделом» между анакротой и катакротой служит верхняя точка первого, как правило, наиболее высокого подъёма на объёмной кривой (точка А), когда сосуд достигает своего наибольшего растяжения. Это точка гемодинамического равновесия между силами, действующими на стенку сосуда с обеих сторон (0 градиент давления).

Точку А не всегда легко находить на пульсовой кривой, поэтому в таких случаях ориентиром служит пересечение с изолинией нисходящей первой производной (точка А₀). В некоторых случаях кривая скорости не достигает изолинии в данной проекции. Это бывает при выраженном гипертоническом типе РЭГ (рисунок VI-5), поэтому в данном случае точка А проецируется на пересечения с изолинией восходящей из У_1- второй производной.

Сила сокращающегося сосуда, направленная внутрь, может действовать как по ходу сосуда, так и ретроградно, т.е. теоретически её вектор может иметь два направления. Рассмотрим все возможные варианты действия данного вектора внутри сосуда.

 

1-й вариант. Ретроградный кровоток отсутствует. В данном случае вектор от стенки сосуда меняет направление на антеградное, т.е. вся сила упругой стенки при сокращении будет направлена на продвижение крови по ходу сосуда.

Если противодействие по ходу сосуда близко к предельному, то скорость сокращения сосудистой стенки будет близка к 0. Сосуд будет оставаться растянутым, и объёмная кривая по шкале времени будет регистрироваться прямой линией, параллельной нулевой и, находящейся на высоте максимального зубца.

Если противодействие по ходу сосуда будет близко к нулю, то скорость возврата сосудистой стенки к нерастянутому состоянию будет близка к максимальной. Объёмная кривая почти мгновенно снизится до 0. Регистрирующее устройство зафиксирует вертикальную линию, достигшую нулевой точки, и в дальнейшем по шкале времени будет регистрироваться горизонтальная линия на нулевой отметке.

Выше очерчены два предела для катакроты, в которых она будут занимать определённое промежуточное положение. Чем выше сопротивление по ходу сосуда, тем более пологий угол наклона. Чем меньше сопротивление, тем угол круче. Иными словами, катакрота объёмной кривой будет представлять собой прямую линию, стремящуюся достичь нулевой отметки под тем или иным углом.

Принято считать, что катакрота достигает изолинии к концу диастолы. Однако, теоретически, достижение нулевой линии возможно и на более раннем этапе. Такой вариант развития событий трудно принять, поскольку в результате этого, из-за утраченной проталкивающей силы, кровь некоторое время будет находиться в состоянии стаза, если на неё не окажет воздействие какая-то иная сила. С трудом верится, что организм позволит иметь паузы в продвижении крови по сосудистой системе. Это противоречит целесообразности и чревато последствиями. Наверняка включатся компенсаторные механизмы по более равномерному распределению проталкивающей силы на всём протяжении диастолы. Однако при определённой патологии возможность такого состояния необходимо учитывать.

С другой стороны, что будет, если пульсовая кривая к концу диастолы не вернётся к изолинии. В данном случае возникает ситуация, когда потенциальная энергия растянутого сосуда, полученная в систолу, не расходуется полностью, а частично переносится на следующий сердечный цикл. В результате этого остаточная энергия будет накапливаться из цикла в цикл, что, в конце концов, приведёт к переполнению сосудов и остановке кровотока.

Поскольку такая катакрота не имеет участков ускорения, то вторая производная будет выглядеть прямой линией, совпадающей с нулевой, а базисная линия скорости, оценивающая среднюю скорость спада катакроты, - прямой линией, расположенной параллельно и несколько ниже изолинии.

Предложенная базисная кривая катакроты является эталоном, и возможна только, если силы сокращающегося сосуда и сердца, направленные на продвижение крови по ходу сосуда, находятся в оптимальном соотношении. Если бы сила сердечного выброса, направленная на продвижение крови, равномерно снижалась, то растянутая сосудистая стенка постепенно бы замещала её накопленной потенциальной энергией. Объёмная кривая опускалась бы прямой линией под некоторым углом к изолинии.

На практике катакрота никогда не выглядит прямой линией, поскольку в разные периоды формируется разными силами. Начальная её часть попадает на продолжающуюся систолу, поэтому взаимодействуют две силы, как со стороны сердца, так и со стороны сокращающегося сосуда. В диастолу продвижение крови по ходу сосуда осуществляется только за счёт накопленного потенциала сосудистой стенки.

Если оценивать реографическую кривую с векторных позиций, то весь сердечный цикл следует разделить на три периода:

Линия катакроты практически никогда не бывает прямой. Во второй и третий период формируются два отрезка этой линии, находящиеся под некоторым углом друг к другу. Таким образом, вышеуказанная линия катакроты А-Д₀ является ломанной (А-П-Д₀).

Поскольку в точке П систола завершается, то высота расположения её относительно базисной линии зависит только от уровня силы противодействия периферических сосудов по ходу кровотока. При оптимальном соотношении сил действия и противодействия катакрота должна полностью совпадать с базисной линией реограммы (точка П будет находиться на ней). При возрастании периферического сопротивления во II период сердечного цикла, прежде всего, вытесняется доля силы сокращающегося сосуда, поэтому сосуд либо замедлит своё сокращение, либо будет продолжать растягиваться.

В позднюю систолу величина вектора пьезометрического давления, направленного в сторону стенки сосуда зависит от:

Оценим взаимозависимость этих категорий друг с другом.

Если периферическое сопротивление снизится, то интегральный вектор перераспределиться в большей степени по ходу сосуда, а потому на растяжение стенки будет направлен меньший вектор давления. Из этого следует, что в период изгнания амплитуда реографической кривой снизится.

Противоположные события произойдут, если периферическое сосудистое сопротивление возрастёт. Возросший вектор бокового давления приведёт к большему растяжению сосудистой стенки, а потому и к увеличению амплитуды реографической кривой в систолу.

Катакротическая линия нормальной реограммы (рис VI-1) наиболее приближена к базисной. При гипертоническом типе (рис VI-5-6) катакрота образует угол вершиной кверху. При гипотоническом типе реограммы вершина угла катакроты в точке П отдаляется вниз (рис VI-7) от эталонной линии. Иными словами, соотношение амплитуд П / П_б будет различным в зависимости от типа реограммы.

Используя эту закономерность можно выйти на оценку прироста или спада величины периферического сопротивления.

Проведём расчёт амплитуды П_б, исходя из пропорции А / А₀_Д₀ = П_б / П₀_Д₀:

П_б = А * П₀_Д₀ / А₀_Д₀ ;

Где П_б – амплитуда, по линии П с проекцией на базисную линию;

А – амплитуда реограммы по линии А₀_А;

П – амплитуда реограммы по линии П₀_П;

П₀_Д₀ – продолжительность диастолы;

А₀_Д₀ – продолжительность катакроты.

Коэффициент спада катакроты равен:

КСК = П / П_б * 100%

Физиологические законы гемодинамики гласят, что, какое бы ни было периферическое сосудистое сопротивление, кровь, изгнанная сердцем в систолу, должна покинуть сосудистое русло в полном объёме к концу диастолы. Этот закон будет соблюдён при любых соотношениях векторов. Из этого следует, что накопленная сосудистой стенкой потенциальная энергия будет полностью израсходована к концу сердечного цикла.

Оптимальная скорость расходования этой энергии должна быть равно-мерной на протяжении всей катакроты. При этом реографическая кривая будет спускаться прямой линией и достигнет нулевой отметки к концу диастолы. Это эталонная катакрота реограммы (А_Д₀). При «нормальном» периферическом сосудистом сопротивлении реографическая кривая будет максимально приближена к эталонной (таблица №1).

Таблица №1. Коэффициент спада катакроты (КСК).

 

Чем интересен коэффициент спада катакроты (КСК)? Он оценивает отклонение реографической катакроты от эталонной (базисной) линии в точке окончания периода изгнания, в которой, естественно, сила, направленная на растяжения сосуда, равна 0. С этого момента скорость расхода накопленной стенкой потенциальной энергии зависит только от величины периферического сосудистого сопротивления.

В позднюю систолу при высоком общем периферическом сосудистом сопротивлении (ОПСС) растянутый сосуд расходует меньше потенциальной энергии, а продолжающаяся систола большее давления перераспределяет в сторону стенки сосуда, препятствуя её сокращению. В результате этого диастола на реограмме начинает свой отсчёт с точки, поднятой кверху от базисной линии. Отмечается прирост КСК. При низком сопротивлении по ходу сосуда происходят противоположные события. Коэффициент спада катакроты снижается. Таким образом, КСК можно использовать как показатель, оценивающий прирост или спад периферического сосудистого сопротивления относительно условной нормы.

Поскольку амплитуда пульсовой кривой на реограмме находится в прямой зависимости от ОПСС, то через поправки с помощью КСК можно выйти на показатели растяжимости, независимые от сопротивления по ходу сосудов. Растяжимость сосудов будет оцениваться при одинаковом для всех условно нормальном периферическом сосудистом сопротивление. В данном случае изменения величин амплитуд на реограммах будет объясняться только свойствами сосудистой стенки – растяжимостью, тонусом, эластичностью.

Интегральный потенциал энергии (E_INT), израсходованной сердцем в систолу, равен сумме энергии, затраченной на продвижение крови по ходу сосуда (E_продв) и на растяжение стенки сосуда (E_растяж).

E_INT = E_продв + E_растяж

В формировании пульсовой волны участвует только та часть энергии, которая направлена в сторону стенки сосуда. В свою очередь при растяжении сосуда в систолу накапливается потенциал (E_накоп), который без учёта затрат на диссипацию приблизительно равен E_растяж. Вся накопленная сосудистой стенкой потенциальная энергия (E_накоп) в систолу, должна быть полностью израсходована в диастолу (E_расход).

E_накоп = E_расход

Систолический объём крови и, естественно, полученный запас энергии распределяется по всем органам и системам по своим закономерностям. Если нам удастся измерить интегральный вектор в начале сосудистой системы в каких-либо условных единицах и найти принципы определения его доли в каждом исследуемом регионе, то мы сможем выйти на расчёты полученных результатов в абсолютных величинах силы, энергии или давления.

Хотел бы ещё раз напомнить, что характеристики таким физическим категориям как сила, давление, энергия даны в I разделе. Поскольку в данном разделе различия между ними не имеют принципиального значения, они, как правило, используются как синонимы.

Для получения параметров сердечного выброса потребуются дополнительные виды диагностики. Это усложнит методику проведения реографического исследования.

Однако ещё сложнее определить долю полученной энергии в каждом конкретном исследуемом регионе, которая зависит не только от ёмкости сосудистого русла последнего, расстояния, пройденного до него пульсовой волной, но и от системы авторегуляции.

Систолический объём крови и, естественно, полученный потенциал энергии распределяется по всем органам и системам по своим законам. Сосуды большинства органов являются мышечно-эластичными, т.е. таковыми, которые имеют определённый базальный тонус, меняющийся за счёт авторегуляции. Из этого следует, что кровенаполнение сосудов того или иного органа может существенно меняться независимо от объёма крови, изгнанной сердцем. Особенно выражена авторегуляция мозгового кровотока, который может долго оставаться достаточно стабильным при весьма существенном падении показателей центральной гемодинамики.

С моей точки зрения, на данном этапе применять абсолютные величины в трактовке реографических кривых практически невозможно. Для того чтобы обойти данную проблему, следует использовать другой методологический подход, приняв интегральный вектор силы сердечного выброса, за некую постоянную величину (const.).

Появляется возможность анализировать реографическую кривую по соотношению давления напора и пьезометрического (бокового) давления через относительное распределение общей силы в виде двух векторов: по ходу, для оценки оттока крови по сосудам, зависимого от периферического сосудистого сопротивления, и в сторону стенки, для оценки растяжимости и сократимости сосудов, их пульсового кровенаполнения. Такие задачи вполне выполнимы и позволяют получить достаточный объём полезной информации.

Реографический метод не даёт нам возможности оперировать абсолютными величинами. Реография не ставит перед собой цели определения запаса энергии, полученной большим кругом кровообращения при работе сердца. Она решает вполне «земные» задачи: через соотношение распределения энергии оценить свойства самого сосуда: растяжимость, эластичность, периферическое сосудистое сопротивление.

Бернулли доказал, что для невязкой и несжимаемой жидкости при установившемся ламинарном потоке в каждой точке системы сумма потенциальной (гидростатическое) и кинетической (пьезометрическое и давление напора) энергии есть для единицы объёма величина постоянная. Часть потенциальной энергии гидростатического давления может превращаться в кинетическую, и наоборот. Это полностью согласуется с законом сохранения энергии, который гласит, что сумма кинетической и потенциальной энергии конкретной частицы - величина постоянная:

E = ½mv² + mgz = const

При этом один вид энергии может переходить в другой, и наоборот.

Итак, общая энергия, полученная в результате сердечного выброса, распределяется кинетической по ходу сосуда, выраженной давлением напора, и потенциальной энергией, формируемой пьезометрическим давлением в сторону стенки сосуда. В результате растяжения сосуда, там концентрируется определённый запас энергии. В диастолу потенциальная энергия растянутого сосуда используется на продвижение крови, вновь превращаясь в кинетическую давлением напора.

В зависимости от поставленных задач степень растяжения сосуда может быть либо эквивалентом пульсового его кровенаполнения, либо – накопленной потенциальной энергии. При оценке сосудистого русла периферических органов более приемлем второй вариант. Измерение энергии можно осуществить в относительных величинах, с последующим использованием их для сравнительной оценки гемодинамических событий при различных вариантах реограмм.

Иные задачи стоят перед трансторакальной реографией, регистрирующей пульсовое кровенаполнение, прежде всего, магистральных сосудов первого порядка – аорты и лёгочной артерии. Последние, в отличие от мелких и средних сосудов, являются эластическими. Участие гладкой мускулатуры в формировании их базального тонуса незначительно, поэтому им можно пренебречь. Между пульсовым кровенаполнением магистральных сосудов грудной клетки и сердечным выбросом существует высокая корреляция, что и используется для косвенного определения показателей гемодинамики.

Какие критерии и показатели следует применять для трактовки реографических кривых? Полагаю, что среди многочисленного количества показателей, используемых для оценки реограмм, пришло время провести инвентаризацию и отбросить большинство из них, не прошедших испытание временем.

Чаще всего используются линейные показатели (амплитудные, временные). Наиболее известные из них: максимальная амплитуда в точке А, высота инцизуры над изолинией в точке И, продолжительность анакроты, катакроты, фазы быстрого изгнания. Несложно понять, что такие параметры не могут служить самостоятельными показателями, поскольку каждый из них зависит не только друг от друга, но и от ряда других величин. Несколько более информативными являются относительные показатели, такие как реографический индекс (отношение максимальной амплитуды к калибровочному сигналу), дикротический индекс (отношение высоты амплитуды в точке И к максимальной амплитуде в точке А).

Более полезную информацию можно получить при использовании двухмерных показателей, амплитудно-временных, таких как скорость, ускорение. Среди них можно выделить максимальную скорость растяжения сосудистой стенки в анакроту, среднюю скорость растяжения сосудистой стенки в анакроту, среднюю скорость спада сосудистой стенки в катакроту и ряд других. Более глубокий анализ этих показателей будет сделан в другом разделе.

Средняя скорость растяжения сосуда в I период (анакроту) рассчитана по формуле

V_I = А / Д₀_А₀;

Средняя скорость сужения сосуда во II период (позднюю систолу) равна

V_II = (А - П) / А₀_П₀ * (-1);

Средняя скорость сужения сосуда в III период (диастолу) равна

V_III = П / П₀_Д₀ * (-1);

Средняя скорость спада катакроты равна

V_кат = А / А₀_Д₀ * (-1).

Где А – амплитуда реограммы по линии А₀_А;

П – амплитуда реограммы по линии П₀_П;

Д₀_А₀ – продолжительность I периода (анакроты);

А₀_П₀ – продолжительность II периода (поздней систолы);

П₀_Д₀ – продолжительность III периода (диастолы);

А₀_Д₀ – продолжительность катакроты.

Таблица №2. Средние скорости подъёмов и спадов по периодам.

 

Несмотря на небольшое количество наблюдений можно проследить ряд закономерностей:

Следует помнить, что средняя скорость растяжения или сокращения сосудистой стенки эквивалентна среднему градиенту силы на данном временном отрезке.

Средняя скорость снижения катакроты равна частному от деления высоты максимальной амплитуды объёмной реограммы в точке А на продолжительность катакроты. Этот показатель будет зависеть как от потенциала растянутой сосудистой стенки, так и от периферического оттока.

Скорость снижения катакроты будет выше, если

Мною приведены физиологические механизмы, от которых зависит скорость снижения катакроты.

Но ведь высокая амплитуда по принятым в реографической семиотике канонам считается признаком гипотонии сосудистой стенки. В связи с этим возникает необходимость вспомнить о таких понятиях, как тонус, сократимость, растяжимость. О них достаточно подробно говорилось выше. Под понятием растяжимость (податливость) следует понимать, способность стенки деформироваться под воздействием силы. Упруго-эластичные свойства того или иного материала заложены в его молекулярной структуре. Стенка сосуда представляет собой систему переплетённых волокон, которые и обладают упруго-эластичными свойствами. Упругие свойства стенок сосуда, как целого, определяются волокнами трёх типов – эластическими, коллагеновыми и гладкомышечными. Все ткани, формирующие сосудистую стенку, имеют свойство растягиваться. Наибольшую растяжимость имеет эластин. Он может растянуться вдвое больше исходной длины. По мере старения, большая часть эластических волокон замещается более жёсткими коллагеновыми волокнами.

Модуль упругости для гладкомышечного волокна примерно такой же, как и для эластина, однако в зависимости от физиологической активности он может меняться. Свойство гладкомышечных волокон менять растяжимость сосудистой стенки под влиянием различных факторов получило название сосудистого тонуса. В зависимости от изменяющихся потребностей организма и изменений уровня кровообращения меняются и упругие свойства сосудистых стенок.

Чем менее растяжим сосуд, тем больший вектор силы направлен на продвижение крови по сосуду.

В сторону более податливой стенки сосуда направлен больший вектор силы, следовательно, больший запас потенциальной энергии там концентрируется. Эластин является резиноподобным материалом, чем больше он растянут, тем с большей силой он сокращает стенку сосуда.

Скорость оттока крови зависит не только от периферического сосудистого сопротивления, но и свойств самой крови, её текучести.

Всё выше изложенное подтверждает, что физиологические процессы не противоречат физическим законам.

Рассмотрим вторую категорию скорости – время.

В живом организме действуют свои физиологические законы, которые мы и проанализируем ниже. Укорочение временного интервала объясняется учащением частоты сердечных сокращений, в результате чего, как правило, возрастает минутный объём сердца. Основной закон гемодинамики гласит, что количеству крови, изгнанной сердцем в систолу, должен быть адекватный отток, т.е. ровно такое же количество должно уйти из артериальной системы. Организм просто обязан включить физиологические механизмы по компенсации возросшего минутного объёма. Это, прежде всего, снижение периферического сосудистого сопротивления, повышение тонуса сосудистой стенки, увеличение скорости кровотока по сосуду. В результате этого основной вектор силы будет направлен по ходу сосуда, амплитуда пульсовой волны снизится.

Если при участившемся сердцебиении минутный объём не возрастает, то это возможно только при более низком систолическом выбросе, что соответственно приведёт к уменьшению вектора силы. Поэтому снизится и его составляющая, направленная в сторону стенки сосуда, а, следовательно, и амплитуда пульсовой волны.

При удлинении катакроты закономерности будут аналогичны, амплитуда пульсовой волны вырастет, и, наоборот, более короткой катакроте будет соответствовать более низкая пульсовая волна.

 

Чтобы рассуждения были более понятными, возьмём в качестве примера реографическую кривую с условно нормальной графикой (рис. №VI-4). Схематизируем её до простых математических фигур, чтобы проще было применить математические расчёты.

Рисунок VI-4. Схема расчётов интегрального потенциала растянутого сосуда.

 

Условно примем, что скорость растяжения сосудистой стенки и пульсовое кровенаполнение сосуда на протяжении всей анакроты одинаковы. В таком случае положительный градиент давления, возникший в результате сердечного выброса, равномерно распределён на протяжении всего указанного периода. Пульсовую кривую в этом случае можно выразит прямой восходящей линией Д_Н_А. Она соединяет начало периода изгнания (Д_Н), где, естественно, пульсовое кровенаполнение равно 0, c точкой А, в которой сосуд достигает своего максимального кровенаполнения.

Итак, мы получили прямоугольный треугольник Д_Н_А₀_А, катетами которого являются Д_Н_А₀, соответствующий продолжительности анакроты, и А_А₀, соответствующий максимальному кровенаполнению растянутого сосуда.

Ещё раз хочу напомнить, что давление действует многовекторно. Поскольку сосуд в своём сечении приблизительно равен кругу, то боковой вектор оказывает давление на стенку по всей окружности. Иными словами, растяжение (как и сужение) сосуда происходит сразу по всему его периметру. Следовательно, предложенная плоскостная реограмма аналогична реограмме в любой другой плоскости, перпендикулярной стенке сосуда.

Объём всякого кругового конуса равен 1/3 произведения площади основания (πr²) на его высоту. Итак, интегральный потенциал энергии растянутого сосуда в анакроту (E_I) наиболее соответствует величине, вычисленной по формуле:

E_I = 1/3 * (π * (А₀_А)² ) * (А₀_Д_Н)

Расчёты интегрального потенциала растянутого сосуда в третий период (диастолу) проводятся по аналогии с первым периодом. Условно примем, что скорость спада сосудистой стенки на протяжении всей диастолы одинакова. Пульсовую кривую в этом случае можно выразит прямой нисходящей линией П_Д_К. Она соединяет начало диастолы П c точкой окончания сердечного цикла Д_К, в которой, естественно, пульсовое кровенаполнение равно 0.

Итак, мы получили прямоугольный треугольник П_П₀_Д_К, катетами которого являются П₀_­­­­­Д_К, соответствующий продолжительности диастолы, и П₀_П, соответствующий максимальному кровенаполнению растянутого сосуда в начале диастолы.

Итак, интегральный потенциал энергии растянутого сосуда в диастолу (E_III) наиболее соответствует величине, вычисленной по формуле:

E_III = 1/3 * (π * (П₀_П)² ) * (П₀_Д_К)

Если в первый период сосудистая стенка только накапливает свой потенциал, в третий – только расходует энергию растянутого сосуда, то во втором периоде взаимодействуют обе эти силы. Прежде чем определить их соотношение рассчитаем суммарный потенциал растянутого сосуда во втором периоде.

Объём всякого усечённого кругового конуса равен произведению 1/3 высоты пирамиды на сумму площади основания (πR²), площади вершины (πr²) и произведения большого и малого радиусов (R*r).

Итак, интегральный потенциал растянутого сосуда во второй период (E_II) наиболее соответствует величине, вычисленной по формуле:

E_II = 1/3 * (А₀_П₀) * (π * (А₀_А)² + (А₀_А) * (П₀_П) + π * (П₀_П)²)

 

В зависимости от типа реограммы соотношение этих сил существенно разниться. Нашей задачей является рассчитать соотношение этих сил. Если в начале периода преобладает сила сердечного выброса, то к концу доминирует сила растянутого сосуда.

Логика рассуждений такова. Суммарный потенциал растянутого сосуда во второй период слагается из потенциала накопления (E_{II_накоп}), связанного с заканчивающимся сердечным выбросом, и потенциала расхода (E_{II_расход}), связанного с начавшимся сокращением растянутого сосуда.

Поскольку вся накопленная сосудистой стенкой потенциальная энергия (E_накоп), должна быть полностью израсходована к концу сердечного цикла (E_расход), то из этого вытекает:

E_накоп = E_расход = (E_I + E_II + E_III) / 2;

E_{II_накоп} = E_накоп - E_I = ( E_I + E_II + E_III) / 2 - E_I ;

E_{II_накоп} = (E_III + E_II - E_I) / 2;

Расчёт интегрального потенциала энергии, израсходованного сокращающимся сосудом во втором периоде (E_{II_расход}) не составит большого труда. В любом случае количество накопленной сосудом энергии (E_накоп) всегда будет равно количеству израсходованной (E_расход).

Хотел бы ещё раз вернуться к показателю КСК. Проведём перерасчёт этих показателей по полученным новым объёмным результатам.

Е_{катакроты} = 1/3 (π * (А₀_А)²) * (А₀_Д_К)

КСК_объём = (E _II + E_III) * 100% / Е_{катакроты}

Рассчитанные по данной формуле показатели КСК_объём дают такие ориентировочные цифры: для нормальной РЭГ – 81,8%, гипотоническая – 51,3%, гипертоническая – 125,5%, значительно гипертоническая – 194,7%. Считаю, что, по сравнению с линейным КСК, этот показатель даёт более точную информацию, и ему необходимо отдать предпочтение.

 

Источник электричества в реографе всегда генерирует ток одинаковой величины. Проводники, кожные электроды, через которые ток проводится к био-тканям, имеют очень низкое сопротивление, а потому потеря электрического потенциала в них ничтожно мала. А вот сопротивление кожи и других тканей, по которым ток идёт к измеряемому участку, у каждого нового обследуемого будет иным. Причём, разница может быть достаточно существенной. По закону Ома сила тока снижается пропорционально величине прироста сопротивления. Следовательно, оценка измеряемого участка ткани в каждом конкретном случае осуществляется при неодинаковых значениях тока I. Это обстоятельство может оказывать влияние на величину импеданса, а потому и входящего в него искомого переменного сопротивления. Если базовое сопротивление возросло, то истинная сила тока на исследуемом участке снизилась, следовательно, амплитуда реографической кривой занижена по той же причине. Использование амплитудных значений реограммы, оценивающей проводимость тока в исследуемом участке биоткани, без поправки на данный фактор может приводить к искажению информации, иногда значительной.

Какой же выход из этой ситуации? Необходимо принять, что при одинаковой силе тока базовое сопротивление исследуемого участка биоткани величина постоянная. При таком подходе доля переменного сопротивления будет пересчитываться пропорционально корректировке базового сопротивления.

Разъясню более подробно. Импеданс для реоэнцефалографических кривых в среднем равен 100 Омам. При отклонении, в каждом конкретном случае, базового сопротивления от этой величины приведём его к стандартной цифре 100 Ом. При этом сделаем перерасчёт и амплитудных значений реограммы пропорционально изменениям импеданса. При таком подходе все реографические показатели будут базироваться на равных исходных условиях. Ещё раз хочу напомнить, что реограмма фактически является кривой электрической проводимости. Электропроводность - физическая величина, обратная электрическому сопротивлению. Поэтому, при снижении базового сопротивления амплитуда реографической кривой будет прирастать.

Например, максимальная амплитуда реограммы А имеет значение 0,07 Ом, базовое сопротивление – 120 Ом. Величина последнего превышает стандартную на 20%. Приведём её к стандартной – 100 Ом, после чего пересчитаем значения реограммы, увеличив амплитуду на те же 20%. Истинная величина амплитуды А станет равна 0,085 Ом.

Такой подход возможен, если расстояние между внутренними электродами будет оставаться стандартно постоянным, поскольку сопротивление всякого проводника также зависит и от его длины.

В предложенной таблице №3 использованы амплитудные значения в точках А и П, в перерасчёте на импеданс равный 100 Омам.

Интегральный потенциал энергии (E_INT), израсходованной сердцем в систолу, равен сумме энергии, затраченной на продвижение крови по ходу сосуда (E_продв) и на растяжение стенки сосуда (E_растяж). В формировании пульсовой волны участвует только та часть энергии, которая направлена в сторону стенки сосуда (E_растяж).

При оптимальном распределении вектор по ходу сосуда равен вектору неправленому в сторону стенки (E_продв = E_растяж).

При повышенном сопротивлении по ходу сосуда в сторону стенки распределится бóльший вектор (E_продв < E_растяж).

При сниженном сопротивлении по ходу сосуда в сторону стенки распределится меньший вектор (E_продв > E_растяж).

 

Таблица №3. Накопление и расход потенциала энергии сосудистой стенкой в систолу.

 

Таким образом, у каждого нового обследуемого, сосудистая стенка растягивается под воздействием неодинакового бокового давления. Это существенно сказывается на её растяжении. Для объективной сравнительной оценки истинной растяжимости сосудов необходимо создать равные условия для всех обследуемых. Для этого необходимо пересчитать все результаты исходя из оптимального распределения энергии по ходу сосуда и в сторону стенки (E_продв = E_растяж). Для этого необходимо использовать показатель КСК_объём.

E_накоп / КСК_объём *100%

Чтобы оценить истинную растяжимость сосудистой стенки необходимо использовать интегральный потенциал энергии, накопленный сосудистой стенкой с поправкой на КСК. При гипотонической реограмме этот показатель близок по значению к нормальному, что указывает на нормальную растяжимость сосудистой стенки. При гипертоническом типе реограммы этот показатель в 4-5 раз ниже, что служит доказательством низкой растяжимости сосудистой стенки.

При нормальной реограмме, как и при гипотонической, накопленный потенциал в анакроту в 5-7 раз выше, чем при гипертонических типах реограмм. Объяснение этому также следует искать в степени растяжимости сосудистой стенки.

В позднюю систолу сосудистая стенка накапливает наибольший потенциал опять же при нормальном типе реограммы. А вот при гипотоническом типе эта величина почти втрое ниже нормальной, и почти вдвое ниже полученной в анакроту. Объяснить это можно возросшим вектором по ходу сосуда из-за низкого периферического сосудистого сопротивления, что привело к снижению вектора в сторону стенки сосуда. А вот при гипертоническом типе реограммы происходят совершенно противоположные события: из-за высокого периферического сосудистого сопротивления вектор в сторону стенки сосуда прирастает, что ведёт к более высокому накоплению потенциала, чем при гипотоническом типе, хотя и ниже, чем в норме.

Расход энергии сосудистой стенкой во второй период при нормальном и гипотоническом типе реограммы приблизительно равны, а вот при гипертоническом типе – почти в 10 раз ниже. Объяснение этому лежит, прежде всего, в высоком периферическом сосудистом сопротивлении.

При нормальном типе реограммы сосудистая стенка сохраняет наибольший потенциал на продвижение крови в диастолу. При гипотоническом типе потенциал, сохранённый для диастолы, почти в 5 раз ниже. А вот при гипертонических типах этот показатель может существенно колебаться в зависимости от степени растяжимости сосудистой стенки и периферического сопротивления по сосуду.

Хотел бы остановиться на распределении накопления и расхода потенциалов по периодам. Наиболее равномерно потенциал накапливается и расходуется при нормальном типе реограммы.

При гипотоническом типе высокая, короткая, остроконечная пульсовая волна может оказывать неблагоприятные эффекты в закрытом пространстве черепной коробки. Вторым неблагоприятным моментом для данного типа реограмм является неравномерность расхода накопленного потенциала во второй третий периоды, что может сказываться на продвижении крови, особенно в конце диастолы.

При гипертоническом типе реограммы накопление и расход сосудистой стенкой потенциальной энергии очень неравномерны. Особенно следует выделить период поздней систолы, когда энергозатраты на продвижение по сосуду крайне низкие, и она перенаправлена преимущественно на накопление.

Но наиболее странно, на первый взгляд, потенциал накопленной энергии расходуется при резко гипертоническом типе реограммы. В период поздней систолы, когда сила сердечного выброса должна участвовать в проталкивании крови по ходу сосуда, она почти полностью распределяется в сторону стенки. Как только сердечная систола заканчивается резко возрастает расход накопленной энергии, переходящей в давление напора. Почему это происходит? Ведь периферическое сосудистое сопротивление должно было остаться прежним.

Хочу дать этому своё понимание событий. Считаю, что в некоторых ситуациях периферическое сопротивление может существенно меняться на протяжении сердечного цикла. Мы привыкли считать, что ОПСС связано с артериолами. В интракраниальном пространстве периферическое сопротивление формируется не только, и может даже не столько ими, сколько сосудами оттока и ликвором, от которых зависит величина внутричерепное давление. При застое в венозной сети и гидроцефалии возрастает внешнее давление на стенку, а потому и накопление потенциала. Направленный в сторону стенки сосуда вектор сердечного выброса наращивает внутричерепное давление. Сдавливаются и вены, плотно прилежащие к артериям. Это создаёт эффект «порочного круга», когда сила сердечного выброса ведёт к приросту периферического сопротивления и затруднению оттока по сосуду. Поэтому после прекращения сердечного выброса создаются более благоприятные условия для оттока.

Несколько слов о средней скорости накопления и расхода энергии сосудистой стенкой. Сравним их по периодам. Они, в основном, подтверждают приведенные выше доводы. Наиболее равномерное распределение потенциала по периодам отмечается при нормальном типе реограммы. При гипотоническом типе – скорость расхода энергии в диастолу в 8 раз ниже, чем в позднюю систолу. При резко гипертоническом типе – скорость отдачи энергии, наоборот, в 8 раз возросла в диастолу относительно второго периода.

Средняя скорость накопления и расхода потенциала сосудистой стенкой рассчитывалась на время продолжительности того или иного периода.

Как же соизмерить предложенные объёмные показатели с традиционными? Считаю, что сделать это необходимо хотя бы на начальном этапе. Реографические виды диагностики использовались в клинической практике более полувека. Накоплен большой информационный материал. Нельзя его отбрасывать огульно. Необходимо выбрать всё, что может помочь в становлении новых подходов реографической диагностики.

Периферическое сосудистое сопротивление оценивается через показатель КСК в %, что позволяет выйти на достаточно достоверные результаты.

Прекрасно понимаю некорректность сравнительной оценки интегрального потенциала, накопленного сосудистой стенкой за период изгнания, с тем или иным линейным показателем, одним из которых является реографический индекс (РИ). Сделано это лишь с одной целью, хотя бы как-то соизмерить объёмные показатели с традиционной трактовкой реограмм. Реографический индекс, по сути, является амплитудным значением реографической кривой в точке А. Его наиболее часто использовали для оценки растяжимости сосудистой стенки. Мною взято 80 реограмм интракраниальных сосудов и конечностей с самыми разными показателями РИ. Произведены расчёты интегрального потенциала энергии, накопленного стенкой сосуда в систолу (E_накоп). Затем вычислено удельное количество объёмного потенциала приходящего на 0,01 РИ в каждом отдельном случае. Средняя величина объёмного потенциала эквивалентная 0,01 РИ приблизительно равна 45мОм²·сек.

Теперь несложно пересчитать:

Если при нормальной реовазограмме РИ приблизительно равен 0,65–0,75, то этому значению соответствует 2900-3300мОм²·сек объёмного потенциала.

Если при нормальной РЭГ в бассейне позвоночной артерии РИ приблизительно равен 0,9–1,1, то этому значению соответствует 4000-5000мОм²·сек объёмного потенциала.

Если при нормальной РЭГ в бассейне сонной артерии РИ приблизительно равен 1,2–1,4, то этому значению соответствует 5400-6400мОм²·сек объёмного потенциала.

Однако приведенные выше прикидочные цифры требуют серьёзных уточнений, поскольку при ручной обработке реографических кривых возможны значительные погрешности.

 

Выше дана характеристика модели катакроты, возникновение которой возможно только, если вектор силы на всём временном отрезке будет направлен только по ходу сосуда. Однако настоящая пульсовая кривая имеет участки спадов и подъёмов относительно базисной линии. Всякие возмущения на этой части кривой указывают на события, происходящие в системе гемодинамики.

Нисходящая часть пульсовой кривой от максимума (точка А) до дикротической впадины (точка И) остаётся наименее изученной с точки зрения физиологии гемодинамических процессов. Если внимательно просмотреть приведенные реограммы, то можно заметить, что у всех отмечены достаточно сходные закономерности. После быстрого спуска объёмная реограмма постепенно становится более пологой, зачастую переходит в очередной подъём, который вновь начинает ускоренно снижаться с переходом в дикротическую впадину (инцизуру). Иными словами, на каждой реограмме на этом участке отмечаются различной степени выраженности выемка и подъём, что указывает на то, что в сердечно-сосудистой системе спорадически возникают силы, меняющиеся как по величине, так и по направлению.

 

2-й вариант. Ретроградный кровоток отсутствует, а по ходу сосуда эпизодически меняется величина силы противодействия.

Если на пульсовой кривой регистрируется выемка (инцизура), то этому можно дать лишь два объяснения: быстрый прирост сил со стороны стенки сосуда или быстрый спад сил противодействия в просвете сосуда.

Поскольку в стенке сосуда не заложено механизмов по резкому приросту расхода накопленного потенциала силы, то объяснение этому следует искать в уменьшении противодействия внутри сосуда. Не вижу механизмов по ходу сосуда, которые за короткий временной интервал могли бы привести к разрежению, падению плотности крови в просвете сосуда. По-видимому, объяснение этому следует искать в другом направлении.

Подъём волны относительно базисной линии, в физическом понимании, является сменой направления вектора силы в сторону стенки сосуда. Наиболее частой причиной появления положительного дополнительного зубца является отражённая волна. Когда продольная волна на пути своего продвижения встречает какое-либо препятствие в виде среды большей плотности, то она отражается в обратном направлении, в результате чего суммируются волны противоположного направления (интерференция). По сути, происходит противодействие двух векторов силы, направленных друг против друга, после чего вектор частично перенаправляется в сторону стенки сосуда. Основной причиной возникновения волн отражения по ходу сосуда являются многочисленные бифуркации. С моей точки зрения, эти волны вносят локальные специфические особенности в зависимости от участка регистрации пульсовой волны.

Правда, некоторые авторы возникновение второй систолической волны (В) на нисходящей части связывают с волной отражения от бифуркации аорты, мотивируя это локализацией данного зубца на временнóй участок сердечного цикла, соответствующий времени, затраченному на прохождение пульсовой волной расстояния к бифуркации и обратно (около 0,2 секунды).

Считаю такую точку зрения ошибочной по ряду причин. Во-первых, за указанное время волна возвращается к началу аорты (месту формирования пульсовой волны). Но ведь пульс можно регистрировать не только там. Если зарегистрировать пульс в брюшном отделе аорты чуть выше бифуркации, то отрезок времени будет вдвое короче, т.е. указанная волна должна находиться почти на верхушке пульсовой волны. Во-вторых, на сосудах шеи или верхних конечностей отражённая волна будет двигаться вдогонку, т.е. в подобной ситуации интерференции просто может не произойти. В-третьих, как объяснить, что вторую систолическую волну находят не только на всех сосудах выше бифуркации, но и на сосудах ног, где регистрируется проходящая волна. Причём, место расположения второй систолической волны на всех сосудах по временнóй шкале одно и то же.

Полагаю, что больше комментариев не требуется. Механизм возникновения этой волны иной, и искать его надо в другом месте.

 

3-й вариант. Основной вектор сохраняет прежнее направление, но эпизодически возникает вектор противоположного направления (ретроградно).

Несмотря на то, что в течение всей систолы основной вектор силы направлен по ходу сосуда, имеются моменты, когда направление вектора частично может измениться против естественного тока крови.

Первый наступает вскоре после завершения фазы быстрого изгнания, когда сила растянутых сосудов начинает брать верх над силой сокращающегося сердца, и связан своим происхождением с событиями в корне аорты. Непосредственно позади каждой из трёх створок аортального клапана в стенке аорты имеются закруглённые карманы, называемые синусом Вальсальвы. В двух из этих карманов находятся устья левой и правой коронарных артерий. Когда после сужения трубка расширяется слишком быстро, наблюдается “отрыв потока”. Если до сужения жидкость двигалась линейно, заполняя всё поперечное сечение, то теперь в центре потока жидкость ускоренно движется по линии тока вперёд, а у стенок образуется разреженное пространство. В фазу быстрого изгнания основная масса систолического выброса с большой скоростью устремляется прямолинейно по ходу аорты, в синусах образуются участки разрежения. Когда скорость выброса снижается, часть крови устремляется обратным током в синусы. В просвете сосуда создаётся некоторое снижение противодействия, что и регистрируется на объёмной кривой впадиной (инцизура С), расположенной в самом начале катакроты.

В качестве доказательства сказанному привожу кривую коронарного кровотока у бодрствующей собаки, полученную в экспериментальных условиях (рисунок II-1). События, происходящие в человеческом сердце, вероятнее всего, аналогичны. Бóльшая часть крови попадает из аорты в русло коронарных артерий, несомненно, во время диастолы. Это естественно, потому что в это время давление в желудочке, и, следовательно, интрамуральное в его стенке значительно ниже давления в аорте. Максимальная скорость объёмного коронарного кровотока попадает на момент закрытия полулунных клапанов. Второй по величине пик объёмного кровотока совпадает с начальным периодом сердечного выброса, когда давление в аорте достигает своего максимума и, вероятно, создаёт достаточный градиент давления для проталкивания крови в коронарные сосуды. На кривой имеется и третий зубец, наименьший, совпадающий по времени с описанным выше событием (отмечен стрелкой). Его гемодинамическая значимость для коронарных артерий мизерна, однако является доказательством того, что в синусе Вальсальвы в это время происходит некий прирост массы крови, создающий градиент давления.

Вторая систолическая волна (волна В) на объёмной кривой образуется в результате интерференции отражённой от корня аорты волны с основным потоком по ходу сосуда, от величины противодействия которого зависима её высота.

Чем выше периферическое сосудистое сопротивление (рисунки VI – 5,6), тем больше энергии перераспределяет в бок стенки сосуда. Кроме того, отсчёт отрицательной (С) и второй систолической (В) волн ведётся от полóго спадающей базисной линии (А-Д₀) на объёмной кривой.

Чем меньше сопротивление по ходу сосуда, тем больший вектор силы перераспределяется по ходу сосуда, тем менее выражены волны С и В на пульсовой кривой. Их отсчёт ведётся от более круто спадающей базисной линии (рисунки VI - 7).

Выяснив механизм возникновения волн С и В, попробуем оценить динамику происходящих процессов с помощью кривых скорости и ускорения.

Первая производная на участке от начала катакроты до инцизуры W-образная, т.е. имеет спад-подъём-спад. Степень выраженности спадов и подъёмов различна в зависимости от типа реографической кривой. При нормальном и гипотоническом типе реограммы она полностью располагается ниже изолинии, что указывает на преобладании сил сокращения над силами растяжения сосудов и доминировании отрицательного градиента давления. В данном случае речь может идти только о спаде или приросте отрицательного градиента давления.

Первая впадина С_с на дифференциальной кривой связана с увеличением скорости сокращения сосудистой стенки в результате частичного оттока крови в синус Вальсальвы и возникшего дополнительного разрежения в просвете сосуда. Её наиболее глубокая точка (extréme min) соответствует наибольшей скорости сокращения стенки сосуда, а потому, и наибольшему отрицательному градиенту давления на данном временном отрезке.

Наиболее глубокий зубец С_с на первой производной регистрируется при гипотоническом типе реограммы, когда отсчёт ведётся от более низко расположенной базисной линии скорости, которая, по сути, эквивалентна среднему градиенту давления на данном временном отрезке.

В норме максимальное ускорение, а потому и максимальный прирост отрицательного градиента давления регистрируется в самом начале катакроты и определяется на восходящей части зубца У_1- в проекции на неё точки А.

Если исходить из логики предыдущих рассуждений, то наибольший прирост отрицательного градиента давления на данном временном отрезке должен быть при гипотоническом типе реограммы, наименьший - при гипертоническом. Но это требует дополнительной проверки.

На нормальной реограмме (рисунок VI-1) зубцы С и В проявляются достаточно хорошо, однако их поиск и трактовку лучше делать по первой и второй производным, используя те же принципы, что и при оценке гипотонической реограммы.

 

В качестве примеров проведём векторный анализ некоторых кривых:

Проведём анализ реограммы данного типа на примере (рисунок VI-5). Предложенная реограмма выглядит монофазной кривой с рудиментарными волновыми колебаниями. Без первой и второй производных анализ такой кривой весьма затруднителен. Точку А, с которой начинается катакрота, по пульсовой кривой найти практически невозможно. На первой производной она наиболее соответствует нижнему экстре́му (точка С_с), когда скорость растяжения сосудистой стенки минимальна, что соответствует наименьшему положительному градиенту давления. Прирост градиента давления в этой точке равен 0, поэтому вторая производная пересекает изолинию снизу (точка А₀).

Сразу же после точки А на пульсовой кривой прослеживается небольшая вмятина. Её нельзя назвать впадиной, потому что сосудистая стенка продолжает идти по пути растяжения. Вмятина же сформировалась в результате некоторого замедления скорости растяжения сосуда, объяснением которому может быть некоторого снижения внутреннего давления в просвете сосуда, ведущего к замедлению темпов прироста положительного градиента давления. Первая производная не пересекает изолинию. Это является доказательством того, что отрицательный градиент давления не возникает, сосудистая стенка не сокращается.

В верхнем экстре́ме второй систолической волны на пульсовой кривой (точка В) первая производная впервые пересекает изолинию в точке гемодинамического равновесия (точка В₀). С этого момента сосуд начинает сокращаться, превалируют силы отрицательного градиента давления. Пульсовая кривая начинает снижаться.

Проанализируем данную реограмму с патофизиологических позиций.

В точке А амплитуда пульсовой кривой хотя и ниже нормальных показателей, но достаточно высокая, что может указывать либо на не слишком большой гипертонус магистральных сосудов, либо на возросший вектор силы в сторону стенки сосуда из-за высокого периферического сосудистого сопротивления. В нашем случае, вероятнее всего, действует второй вариант.

Небольшая вмятина на пульсовой кривой указывает на небольшой спад давления в просвете сосуда, связанный с ретроградным оттоком некоторого количества крови в синус Вальсальвы. Высокое давление в просвете сосуда, обусловленное большим сопротивлением по ходу оттока крови, не позволило сосудам сократиться, поскольку превысило силу противодействия со стороны стенки сосуда.

Высота волны В обусловлена прежде всего тем, что базисная линия пульсовой кривой на данном временном отрезке не имеет спада, находится на высоте, полученной в анакроту. Поскольку в это время систола продолжается, то, вполне возможно, она даже прирастает.

Линия первой производной, соответствующая средней скорости растяжения сосуда, на данном временном отрезке находится выше изолинии. Вектор силы, возникший в результате отражения волны от корня аорты, встретив очень высокое сопротивление по ходу сосуда, практически полностью перенаправился в сторону стенки, ведя свой отсчёт от высокорасположенной базисной линии.

Клинико-диагностическое заключение должно выглядеть приблизительно так: Резко гипертонический тип реограммы по смешанному магистральному и периферическому (дистальному) типу.

Здесь используется традиционная терминология, по поводу которой разговор будет ниже.

Рисунок VI-5 (а, в, с)

 

Нулевая линия дважды пересекает средний положительный зубец Вс W-образной кривой скорости. Такой вариант возможен, если базисная линия скорости расположена под изолинией достаточно близко к ней. Прирост скорости, возникший после отражения от корня аорты волны, создаёт условия для пересечения первой производной нулевой линии. Вновь возникает положительный градиент давления, который приращивает амплитуду пульсовой кривой.

На второй производной зубец У₂₊ в своей верхней точке оценивает максимальный прирост положительного градиента давления второй систолической волны.

Рисунок VI-6 (а, в, с)

 

На второй производной зубец У₂₊ в своей верхней точке оценивает максимальный спад отрицательного градиента давления второй систолической волны. Точки С и В находят по пересечению зубца У₂₊ с изолинией в точках С₀ и В₀.

Рисунок VI-7 (а, в, с)

 

Независимо от типа реограммы после точки В сосуд сокращается, превалирует отрицательный градиент давления. На пульсовой кривой идёт спад. Кривая скорости обязательно фиксируется ниже изолинии. Этому временному отрезку на первой производной соответствует второй отрицательный зубец К_с.

В еxtréme min зубца К_с регистрируется наибольшая скорость сокращения сосудистой стенки, обусловленная окончанием систолы. С этого момента сила растянутых сосудов доминирует над всеми остальными силами. Заканчивается изгнание крови из левого желудочка. Принято считать, что в точке К_с завершаются фаза быстрого изгнания и всей систолы.

На кривой ускорения появляется второй отрицательный вектор ускорения У_2-. С моей точки зрения, моменту завершения сердечной систолы наиболее соответствует точка П_у на кривой ускорения, соответствующая extréme min зубца У_2-, когда регистрируется наибольший прирост скорости, а потому, и отрицательного градиента давления. Объяснение этому может быть только в резком спаде внутреннего сопротивления после прекращения сердечного выброса.

При сокращении сила растянутых сосудов распределяется как по ходу (основной базисный вектор), так и в сторону аортального клапана, который пока ещё остаётся открытым. Время от окончания изгнания крови из желудочков до закрытия полулунных клапанов получило название протодиастолы.

В закрытии створок аортального клапана участвуют не только силы, действующие со стороны растянутых сосудов, но и само сердце, которое активно увеличивает объём камер, создавая присасывающий эффект. Давление в левом желудочке падает ниже давления в аорте. Это приводит к частичному оттоку крови из аорты ретроградно, вызывающему резкое закрытие аортального клапана. Появившееся свободное пространство даёт прирост градиента давления в пользу сосудистой стенки, что проявляется увеличением скорости спада пульсовой кривой.

С момента закрытия полулунных клапанов прирост скорости сокращения сосудов быстро падает, дифференциальная кривая приближается к изолинии снизу и пересекает её. На пульсовой кривой эта точка соответствует extréme min дикротической выемки или инцизуры И, в которой регистрируется нулевая скорость сокращения сосудистой стенки.

Высота расположения инцизуры пульсовой кривой над изолинией зависит от типа реограммы. На гипертонической реограмме точка И отдаляется от нулевой линии, поскольку базовая линия катакроты, от которой ведёт свой отсчёт инцизура, имеет пологий спуск. На гипотонической реограмме пульсовая кривая круто спускается, поэтому инцизура больше приближена к изолинии.

На первой производной максимальная скорость сокращения стенки сосуда регистрируется в точке К_с, затем отрицательный градиент давления начинает снижаться, приближаясь к изолинии, и в точке пересечения с изолинией (точка И₀) достигает нулевой отметки.

При гипертоническом типе реограммы первая производная не всегда достигает нулевой отметки в месте проекции точки И. Объяснение этому следует искать на пульсовой кривой, на которой инцизура и последующий диастолический подъём слабо дифференцированы. По сути, инцизуры как таковой нет, а есть неглубокая вмятина. Поскольку после точки И пульсовая кривая продолжает снижаться, то на первой производной не возникает положительного градиента давления, а потому кривая скорости не пересекает изолинии. В данном случае инцизура проецируется на первую производную в месте её наибольшего приближения к изолинии, в которой регистрируется наименьший градиент давления. При таком типе реограммы точку И₀ находят по второй производной, в месте пересечения её с изолинией, где регистрируется нулевой прирост градиента давления.

Более подробно проанализируем зубец У_2- на кривой ускорения, который оценивает максимальный прирост градиента давления в протодиастолу, когда систолический выброс завершён. В норме при закрытии клапана аорты около 5% (около 3-4 мл) крови возвращается в полость желудочка. В результате прогиба парусовидных створок аортального клапана в сосудистой системе возникает дополнительное пространство. Если принять это пространство за полусферу с сечением равным диаметру аортального клапана (около 2.5 см), то по формуле 2/3pR³ несложно рассчитать, что оно сможет принять около 3-4 мл (3.6 см³) крови. Появившееся свободное пространство даёт прирост градиента давления в пользу сосудистой стенки, что проявляется увеличением скорости спада пульсовой кривой.

С некоторыми допущениями можно принять, что прирост отрицательного градиента давления в этой фазе достаточно постоянен. Значит амплитуда зубца У_2- не должна иметь больших колебаний. Если амплитуда данного зубца выходит из коридора нормы, то причина этому заложена в сократительной способности сосудистой стенки.

Такой подход позволяет выйти на такой показатель, характеризующий сократительную способность стенки сосуда, как эластичность.

Отражённая от закрывшихся полулунных клапанов волна наталкивается на инерцию медленно текущей крови по ходу сосуда. В результате интерференции образуется диастолическая волна Л. Чем больше периферическое сосудистое сопротивление, тем она выше, поскольку бóльший вектор перенаправляется в сторону сосудистой стенки и образованная волна проецируется на более высокую базисную линию катакроты.

На первой производной появляется положительный зубец, величина которого пропорциональна возникшей силе положительного градиента давления. При выражено гипертоническом типе реограммы на данном временном отрезке первая производная может регистрироваться ниже изолинии, что указывает на то, что положительный градиент давления не возникает и сосудистая стенка не растягивается. Это может служить доказательством гипертонуса магистральных сосудов, хотя определённую роль может сыграть и снижение периферического сосудистого сопротивления по ходу сосуда.

Однако более наглядная информация прослеживается на второй производной, на которой в этот временной отрезок формируется положительный зубец У₃₊. В одних случаях он отмечает прирост положительного, других – спад отрицательного градиента давления. Но, в любом случае этот зубец отражает прирост градиента давления в сторону сосудистой стенки. Его формирование происходит вследствие отражения волны от закрывшихся полулунных клапанов.

В результате событий в протодиастолу произошёл прирост положительного градиента давления. Часть энергии утрачена при возврате крови в левый желудочек, часть – диссипировала в тепловую энергию при захлопывании полулунных клапанов. Оставшаяся энергия сформировала отражённую волну, силовой потенциал которой можно принят за некую стабильную величину. Имеется в виду, что сила отражённой волны всегда одна и та же, независимо от типа реограммы. Поскольку периферическое сосудистое сопротивление также осталось неизменным на протяжение протодиастолы, то прирост положительного градиента давления в сторону стенки сосуда зависит только от свойств самой стенки, а именно её растяжимости. Чем больше растяжимость сосудистой стенки, тем бóльший вектор отражённой волны направлен в её сторону.

Диастолическая волна постепенно снижается. Последняя четверть сердечного цикла на объёмной кривой большинства сосудов характеризуется полого спускающейся базисной линией с небольшими отражёнными волнами локального значения. К концу диастолы она достигает нулевой отметки. Амплитуды первой и второй производных незначительно колеблются в ту или иную сторону от изолинии.

Сделаем несколько выдержек из приведенных выше рассуждений, которые следует принять в виде постулатов, чтобы выйти на наиболее реальную изоэлектрическую линию.

Рисунок VI-8 (а, в, с)

 

На реографической кривой изобилует большое количество интерферирующих волн, а конечная фаза диастолы зачастую занята пресистолической волной, что делает практически невозможным нахождение истинной изолинии, соответствующей нулевому растяжению волокон сосудистой стенки. В этой ситуации следует подобрать вариант с наименьшей погрешностью, которому более всего соответствует линия, проведенная по наиболее низко расположенным точкам объёмной реограммы независимо от места их локализации.

Однако здесь имеется исключение. Это время протодиастолы, когда возникает вектор, направленный в сторону левого желудочка. В его происхождении задействованы две силы: одна со стороны сокращающейся стенки сосуда, вторая в результате создания отрицательного давления в просвете левого желудочка (присасывающий эффект). Такое явление при выраженной гипотонии сосудистой стенки может привести к прогибу сосудистой стенки внутрь сосуда. Следовательно, в данном случае инцизура может пересечь изолинию. В этой ситуации использование наиболее глубокой точки инцизуры для нахождения изолинии, вызывает определённые сомнения.

Выше (рисунок VI-8) приведен пример реоэнцефалографической кривой у больного с вертебробазилярной недостаточностью, полученной при повороте головы.

Где провести изолинию? Некоторые авторы предлагают для этого использовать самую низкую точку в последней четверти сердечного цикла. В нашей ситуации она полностью занята большой пресистолической волной. Если мы используем минимум между диастолической и пресистолической волнами (Д₁), то получим инцизуру И, глубоко расположенную ниже изолинии. Какое-либо физиологическое объяснение этому найти нельзя. При визуальной оценке несложно увидеть, что перед нами гипотонический тип реограммы, которому должен соответствовать достаточно высокий максимальный зубец А, однако при использовании предложенной изолинии, последний по своей амплитуде больше подойдёт для гипертонического типа. И, наконец, на реоэнцефалограмме без поворота головы подобных изменений нет. Следовательно, предложенная пульсовая кривая, сформировалась не в результате проведения первичной волны, а связана с событиями в самом сосуде данного региона. Значит, присасывающий эффект сердца, к данной ситуации не имеет отношения.

Протодиастола - самая короткая фаза сердечного цикла. Её продолжительность составляет около 0,04 сек. За это время давление в желудочках снижается приблизительно на 15 мм.рт.ст. Это приводит к ускоренному кровотоку в сторону сердца и быстрому захлопыванию аортального клапана, которой на объёмной реограмме соответствует наиболее глубокая точка инцизуры (И). Обычно, инцизура не пересекает нулевую линию, однако при гипотонии это регистрируется. В связи с этим возникает вопрос – истинный ли это прогиб сосудистой стенки внутрь или нулевая линия завышена. Даже если допустить, что сосудистая стенка под влиянием некоторого вакуума в протодиастолу прогибается в просвет сосуда, то значимость этого феномена невелика, и им можно пренебречь.

Время возникновения этой волны – конец диастолы. В магистральных сосудах артериального русла пульсовое давление достигает своего минимума. Единственным источником силы для продвижения крови по сосудам является растянутая сосудистая стенка, потенциальная энергия которой близится к концу. Объяснить возникновение достаточно высокой волны в этой фазе событиями, заложенными в самом сосуде, не представляется возможным.

Некоторые авторы пытаются объяснить это гармоническими затухающими колебаниями волн отражения. Мне кажется, значимость этого явления в сосудистом русле несколько завышена. Всякая отраженная волна всегда заметно ниже той, которая её породила, поскольку при всяком столкновении происходит частичная её диссипация (рассеивание энергии). Когда мы говорим об отражении волны, то имеем ввиду продольную волну, которая, направляясь ретроградно, сталкивается со встречным потоком. В результате интерференции образуется поперечная волна, регистрируемая нами как пульсовая. От бифуркации аорты отражается не более 20% общей массы крови, остальная проводится. В других сосудах процент, скорее всего, не выше.

Если подходить к бифуркациям с точки зрения целесообразности, то, думается, они не предназначены для регуляции гемодинамических процессов. Скорее всего, это издержки всякого разветвлённого трубопровода.

Когда говорят о каком-то гармоническом затухающем процессе, то подразумевают, что волна достигает некоего “противоположного берега”, отражается от него, возвращается к этому, затем обратно. Иными словами, туда и обратно до полного затухания. Сосудистая система извилиста и разветвлена. Если “этим концом” являются бифуркации, то от чего будут отражаться волны “в том конце”? У аорты есть её корень. А в других сосудах? Они что, тоже будут продвигаться к корню аорты?

Пресистолическая волна совпадает с последней фазой сердечного цикла - систолой предсердий, продолжительность которой около 0,1 секунды. При сокращении левого предсердия в желудочек поступает не более 15-20% необходимой крови (около 12 мл). К концу систолы предсердий давление в левом желудочке не превышает 10-12 мм.рт.ст., в то время как диастолическое давление в аорте достигает 70-80 мм.рт.ст. Полулунные клапаны закрыты. Существенных колебаний стенок левого желудочка и створок аортального клапана не происходит, что подтверждается эхокардиоскопией. Таким образом, они никоим образом не задействованы в формировании пресистолической волны.

Рисунок VI-9 (а, в, с)

 

Давление в правом предсердии равно давлению в магистральных венах и несколько ниже, чем в левом предсердии. Оно составляет в среднем около 2-4 мм.рт.ст., максимальное – не более 6-8 мм.рт.ст., минимальное – не ниже -3 мм.рт.ст. Пульсовое венозное давление при сокращении правого предсердия не превышает 3 мм.рт.ст., а в сосудах шеи оно ещё ниже.

Упругое сопротивление венозных стенок значительно ниже артериальных, и величина его в большей степени зависит от состояния тонического напряжения мышечных элементов, что резко сказывается на изменении ёмкости венозного резервуара. Упругое состояние вен, согласно общему закону, определяет скорость распространения пульсовой волны, которая в 2-3 раза ниже, чем в артериях. Пульсовая волна распространяется ретроградно, и в области нижней полой вены её скорость в норме составляет около 2 м/сек.

Сокращение предсердий начинается ближе к концу желудочковой диастолы и по времени совпадает с зубцом P на ЭКГ. Энергия при этом тратится преимущественно на продвижение венозной крови в правый желудочек. Некоторая часть её распространяется ретроградно в полые вены и магистральные венозные сосуды, создавая при этом пульсовую волну в виде положительного зубца на флебограмме. Этот зубец наиболее отчётливо проявляется на магистральных венах шеи, лёгких, печени. Его практически никогда не находят на магистральных венах конечностей.

Рисунок VI-10 (а, в, с)

 

Что общего между предсердной венозной волной и пресистолической волной на реограмме? Время и место. Они регистрируются в тех же регионах в одно и то же время. Пресистолическую волну никогда не фиксируется на аорте и сосудах конечностей, т.е. это явление не носит системный характер, а связано с определёнными областями.

Реограмма регистрирует меняющееся пульсовое кровенаполнение определённой области, в которых пульсируют не только артерии, но и вены. Тем более, к концу диастолы пульсация артерий может быть ничтожно малой, особенно на фоне гипотонии. А именно при гипотонии пресистолическая волна наиболее ярко выражена.

Несмотря на достаточную убедительность доказательной базы, у данной версии есть некоторые контраргументы, вносящие сомнение в её полную достоверность.

Первый контраргумент связан с нестабильностью регистрации пресистолической волны по временнóй шкале. Она может наползти на последующую пульсовую волну, и, наоборот, отдалиться от неё. Но этому можно дать достаточно убедительное объяснение. Регистратор расположен не непосредственно в месте формирования венозной волны, а на определённом расстоянии, до которого последняя должна дойти. Время, затраченное на прохождение этого пути, зависит от свойств сосуда и скорости распространения пульсовой волны, которые могут меняться в тех или иных условиях.

Второй контраргумент – это регистрация пресистолической волны на сфигмограмме, на которой никак не может быть зафиксирована венозная волна. Так уж и не может? Кто даст гарантию, что сфигмограмма на шее, где её наиболее часто записывали, зарегистрировала “чистый” артериальный сигнал? Крупная вена находится рядом. Кто-нибудь пробовал получить запись артериального пульса с последовательным пережатием артериального и венозного сосуда? Кто-нибудь пробовал получить одновременную запись сфигмограммы и флебограммы одной и той же области?

Если всё-таки пресистолическая волна - артериальное явление, то можно этому дать ещё одно объяснение. Мы спокойно принимаем, что пульсирующая артерия трансмурально передаёт часть своей энергии на продвижение крови в прилежащей вене. Почему нельзя допустить обратное, что пульсирующая вена, имеющая пульсовое давление 3-4 мм.рт.ст., трансмурально влияет на близлежащую гипотоничную артерию с пульсовым давлением не выше 1 мм.рт.ст.? А если сокращённая стенка при гипотонии достигает изолинии раньше, может за счёт этой силы и осуществляется продвижение крови по сосудам?

Рассмотрим подъём реографической кривой в анакроту на нормальной реограмме. Поскольку на такой реограмме в позднюю диастолу нет дополнительных волн, мы можем проследить графику объёмной реограммы, так сказать, «в чистом виде» (рисунок VI-1). От изолинии реограмма начинает подъём с постепенного «разгона», что, видимо, обусловлено некоторой инерцией нерастянутого сосуда. В средние три четверти анакроты сосуд растягивается со скоростью, близкой к максимальной, поэтому регистрируется почти прямая линия. В конце подъёма скорость вновь падает, поэтому на реограмме регистрируется короткий участок «торможения». Точки Д₀, М (проекция точки М_с на объёмную кривую) и А находятся на одной линии.

Какие же практические выводы напрашиваются из этого наблюдения? Если провести прямую линию из точки А через точку М до пересечения с изолинией, то в этом месте и должна находиться искомая точка Д₀.

Переведём эту мысль в математическую формулу:

  Д₀_А₀              М₀_А₀

——— = ———————— ;

 А₀_А        (А₀_А) – (М₀_М)

Отношение продолжительности анакроты к высоте максимальной амплитуды реограммы в точке А равно отношению временного отрезка между точками М₀ и А₀ к разности амплитуд реограммы в точках А и М. Если мы рассчитаем продолжительность анакроты (Д₀_А₀), то несложно будет найти точку начала анакроты, отсчитав её от точки А₀.

 

                  (М₀_А₀) * (А₀_А)

Д₀_А₀ = ──────────────

                   (А₀_А) – (М₀_М)

В сложных случаях данный метод нахождения точки начала отсчёта реограммы даёт результаты с наименьшей погрешностью. Пробные расчёты показали, что разница между продолжительностью анакроты полученной эмпирическим путём и рассчитанной по формуле не превышает 5%. В абсолютных цифрах разница не превысила 4-5мс.

 

Конец VI раздела.